nLab higher observational type theory

Higher observational type theory is currently a work in progress, supported by only one scientific publication, that started to be advertised in the community of type theory in 2022. For most of its claims, at current stage, we only have a collection of talks and slides, the reader should keep this information in mind while reading this page.

Idea

Where the idea of (non-higher) observational type theory is to equip all type formation rules (notably dependent functions, dependent pairs and inductive constructions) with their dedicated notion of structure preserving definitional equality — namely: component-wise, ie. homo-morphic, hence: “observational” —; the idea of higher observational type theory (or ‘HOTT’) is to do the same for propositional equality hence for identification types used in homotopy type theory (where types behave like *higher* homomotopy types, whence the qualifier “higher”).

Concretely:

• the “observational” principle for identification of dependent functions is to say that these are dependent functions of identifications of arguments and values (a statement otherwise known as function extensionality),

• the “observational” principle for identifications of dependent pairs is to say that these are dependent pairs of identifications of factors,

and in ordinary univalent homotopy type theory this form of the “structure identity principle” follows as a type equivalence between identification types:

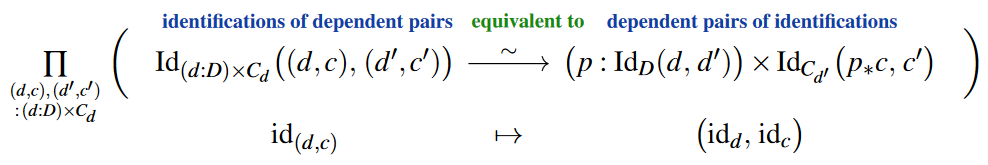
The idea of higher observational type theory is to make these and analogous structural characterizations of identification types be part of their definitional inference rules, thus building the structure identity principle right into the rewrite rules of the type theory.

In such a higher observational theory, in particular also the univalence axiom would be a definitional equality and hence would “compute”.

This most desirable property of any homotopy type theory has previously been accomplished only by cubical type theories. However, cubical type theories achieve this only by adding syntax for auxiliary/spurious interval types with rewrite rules which encode technical detail that has no abstract motivation other than making the univalence axiom compute and which one would rather keep out of the syntactic logic and instead relegate to the construction of categorical semantics.

The hope is therefore that higher observational type theory would provide a type system which achieves both:

1. its syntax is logically cleaner than that of cubical type theories, since there isn’t a interval primitive;

2. its inference rules for identification types make the univalence axiom be a computable function, as it is in cubical type theories and unlike the case for Martin-Löf dependent type theory.

Since higher observational type theory is still work in progress, there being as yet no formally specified theory called ‘HOTT’ in the literature, the extent to which this hope is being realized should be explored in the references below.

HOTT has been motivated by the philosophical claim that Book HoTT does not provide a foundation for mathematics that is truly autonomous from set theory (Shulman 24).

Definition

Using internal parametricity

One version of higher observational type theory is an extension of dependent type theory with

• internal binary parametricity in the form of bridge types and heterogeneous bridge types, with a symmetry operation on higher-dimensional bridge cubes.

• higher coinductive types that modify the whole context by replacing variables in the context with higher-dimensional bridge cubes. This means that, like multimodal dependent type theory and unlike Martin-Löf dependent type theory, assuming an axiom term of type $A$ is not the same as working in the context of a variable of type $A$ (see here for more information)

• a fibrancy predicate higher coinductive type that makes the bridge types into identity types, cogenerated by

  • two transport functions,

  • two dependent functions which give witness that each element is heterogeneously bridged with its transported version,

  • a witness that heterogeneous bridge types of fibrant types are also fibrant

See also

• observational type theory

• homotopy type theory

• Martin-Löf type theory

• cubical type theory

References

Higher observational type theory was introduced as joint work of Thorsten Altenkirch, Ambrus Kaposi and Michael Shulman, first presented in:

• Michael Shulman, Towards a Third-Generation HOTT:, talk at Homotopy Type Theory at CMU (2022) [part 1: slides, video; part 2: slides, video; part 3: slides, video]

• Agda code: github.com/mikeshulman/ohtt

• Mike Shulman, Higher Observational Type Theory: An autonomous foundation for univalent mathematics (slides)

Additional talks on higher observational type theory was presented at the Center for Quantum and Topological Systems in:

• Thorsten Altenkirch, Univalence Without an Interval, talk at Homotopy Type Theory and Computing – Classical and Quantum, Center for Quantum and Topological Systems (video)

• Mike Shulman, Towards an Implementation of Higher Observational Type Theory, talk at Homotopy Type Theory and Computing – Classical and Quantum, Center for Quantum and Topological Systems (video)

The following article is about a fragment of higher observational type theory:

• Thorsten Altenkirch, Yorgo Chamoun, Ambrus Kaposi, Michael Shulman, Internal parametricity, without an interval, Proceedings of the ACM on Programming Languages (POPL) 8 (2024) 2340-2369 [arXiv:2307.06448, doi:10.1145/3632920]

The authors of the above article write:

We presented a type theory with internal parametricity, a presheaf model and a canonicity proof. It can be seen as a baby version of higher observational type theory (HOTT). To obtain HOTT, we plan to add the following additional features to our theory:

• a bridge type which can be seen as an indexed version of $\forall$,
• Reedy fibrancy, which replaces spans by relations,
• a strictification construction which turns the isomorphism for $\Pi$ types into a definitional equality (in case of bridge, we also need the same for $\Sigma$),
• Kan fibrancy, which adds transport and turns the bridge type into a proper identity type. This would also change the correspondence between $\forall U$ and spans into $\forall U$ and equivalences.

Philosophical motivation for HOTT as an autonomous foundation is given in:

• Mike Shulman, From HoTT to HOTT: Autonomy in new foundations for mathematics [slides].

Parametric and higher observational type theory in Narya:

• Parametric Observational Type Theory, Narya documentation. (web)

• Higher datatypes and codatatypes, Narya documentation. (web)

• Higher Observational Type Theory, Narya documentation. (web)